درجه آزادی در مدل سازی معادلات ساختاری

متاسفانه در برخی از جلسات دفاع از پایان نامه و پروژه های مختلف دیده شده است که برخی از اساتید داور  دلیل عدم تسلط بر مباحث آماری و نرم افزار های مدل سازی معادلات ساختاری ایراد غیر واردی را به دانشجویانی که تحلیل آماری خود را با نرم افزار هایی مثل لیزرل و ایموس انجام داده اند، وارد کرده اند و بعضا حتی اتهام داده سازی و دستکاری در مدل و داده ها را به دانشجویان وارد کرده اند.

یکی از این ایرادات معمول، پرسش در مورد میزان درجه آزادی یا df مربوط به مدل ها در مدل سازی معادلات ساختاری می باشد. در مقاله قبل پیرامون p value در نرم افزار های مدل سازی معادلات ساختاری بررسی شد و بیان شد که مقدار chi square با درجه آزادی مورد تعدیل قرار می گیرد.

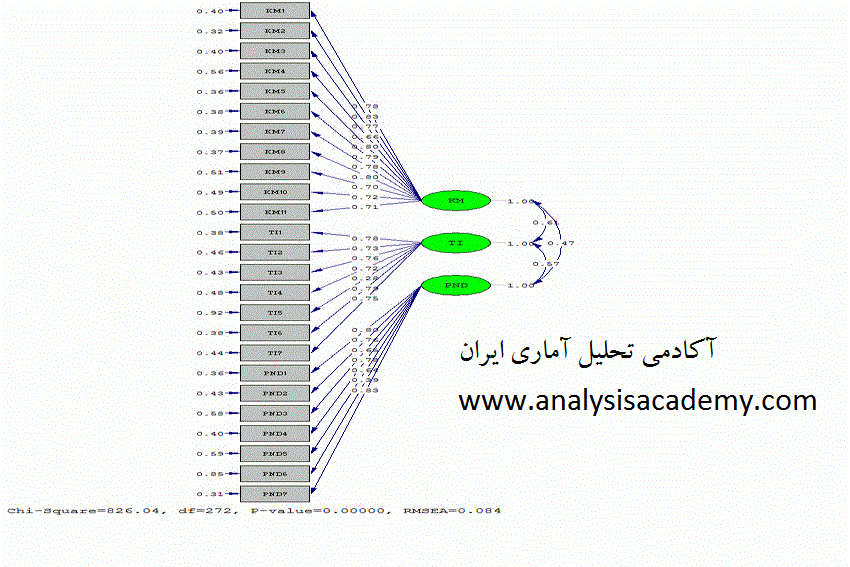
اما مسئله این است که درجه آزادی در مدل سازی معادلات ساختاری چگونه محاسبه می شود. چون متاسفانه مواردی از تجربیات دانشجویان آکادمی تحلیل آماری ایران بیان شده است که در جلسات دفاع استاد داور پرسیده که چرا درجه آزادی df= n-1 نیست. به مثال که عکس آن را مشاهده می کنید توجه نمایید.

در مدل اندازه گیری زیر که در نرم افزار لیزرل اجرا شده است ما سه متغیر مکنون و 25 متغیر آشکار یا سوال داریم و در نهایت این مدل برای حجم نمونه ای با تعداد n=288  نفر اجرا شده است. حال در جلسه دفاع اگر استاد داوری پرسش کند که حجم نمونه شما 288 عدد است و چرا درجه آزادی 272 نفر شده است چه پاسخی باید داد. حتی در برخی از مدل ها ممکن است که درجه آزادی از تعداد حجم نمونه بیشتر خواهد شد. پاسخ ساده است. در آمار برای آزمون های مختلف درجه آزادی فرمول های متفاوتی دارد و کافی است ما به دقت معادله لازم برای محاسبه درجه آزادی آزمون مربوطه را نوشته و آن را حساب نماییم.

در مدل سازی معادلات ساختاری درجه آزادی از فرمول زیر محاسبه می شود.

Df = ½ (p)(p+1) – k

در این فرمول:

P  تعداد متغیر های آشکار یا مشاهده شونده است و k تعداد پارامتر هایی است که نرم افزار قرار است در مدل محاسبه نماید. میبینیم که حجم نمونه در اینجا هیچ نقشی ندارد و تنها کافی است ما به درستی تعداد متغیر های آشکار و تعداد پارامتر هایی که مدل قرار است مورد محاسبه قرار دهد را حساب کنیم.

در مدل زیر ما 25 سوال یا همان 25 متغیر آشکار یا مشاهده شونده داریم، بنابراین بجای p عدد 25 قرار می گیرد. اما اگر خوب به مدل نگاه کنیم تعداد پارامتر هایی که نرم افزار محاسبه کرده است مشخص است.

در این مدل چون 25 سوال داریم بنابراین 25 ضریب بار عاملی و نیز 25 خطای اندازه گیری برای مدل محاسبه می شود. همچنین اگر به متغیر های مکنون در مدل اندازه گیری نگاه کنیم 3 ضریب همبستگی بین متغیر های مکنون نیز باید مورد محاسبه قرار گیرد. بنابراین 25+25+3 برابر با 53 می شود که این همان تعداد پارامتر هایی است که این مدل محاسبه می نماید. بنابراین:

Df = ½ (p)(p+1) – k

Df = ½ (25)(25+1) – 53 = 272

می بینیم که این همان عددی است که نرم افزار به عنوان درجه آزادی محاسبه کرده است. امید است که این مقاله نیز مفید واقع شده باشد.

 

محسن مرادی

بعد از خواندن مقاله بالا خواندن مطالب زیر توصیه می شود:

• نام علمی پارامتر های مدل سازی معادلات ساختاری

• روش های بررسی اعتبار مدل در مدل سازی معادلات ساختاری
  

• اشتباهات رایج در تعریف مدل در مدل سازی معادلات ساختاری​

• دلایل استفاده از رویکرد واریانس محور در مدل سازی معادلات ساختاری
  

مطالب سایت و کانال بدون ذکر منبع استفاده نشود.