آزمون t با دو نمونه مستقل به زبان ساده
این آزمون، میانگین دو گروه از پاسخ گویان را با یکدیگر مقایسه می کند. به عبارتی دیگر در این آزمون، میانگین های بدست آمده از نمونه های تصادفی مورد قضاوت قرار می گیرد. بدین معنی که از دو جامعه مختلف، نمونه هایی اعم از اینکه تعداد نمونه مساوی یا غیر مساوی باشند، به طور تصادفی انتخاب کرده و میانگین های آن دو جامعه را با هم مقایسه می کنیم.(منصور فر، 1384: 201)
این روش بر پایه ی توزیع نرمال t بوده و برای نمونه های کوچک نیز، زمانی بهترین کاربرد را دارد که داده های متغیر مقایسه شونده در گروه های مستقل از توزیع نرمال برخوردار باشد.
پیش فرض های آزمون t با دو نمونه مستقل
الف) متغیری که میانگین آن در دو گروه مستقل مقایسه می شود باید کمی باشد(یعنی مقیاس آن فاصله ای یا نسبی باشد)
ب) مقیاس متغیری که در آن مقایسه انجام می شود باید کیفی و در سطح اسمی(دو وجهی) باشد.
ج) متغیری که در آن مقایسه میانگین انجام می شود باید مستقل و از دو جمعیت متفاوت باشند.
د) توزیع داده های متغیری که میانگین آن در دو گروه مستقل مقایسه می شود باید نرمال باشد.(مرادی، 1395)
خوب اکنون فرض می کنیم موضوع پژوهشی داریم که قصد داریم در آن سازه ای با عنوان عوامل استرس زا (Creator) را در بین دانشجویان دختر و پسر مورد مقایسه قرار دهیم. بنابراین فرضیه ای با این گزاره مشاهده می کنیم
«سازه عوامل ایجاد کننده استرس در بین دانشجویان آقا و خانم تفاوت دارد.»
ابتدا باید بررسی کنیم آیا پیش فرض های بیان شده برای انجام آزمون پارامتریک مقایسه میانگین برای دو نمونه مستقل را داریم یا خیر؟
شرط اول) سازه عوامل ایجاد کننده استرس متغیری کمی است زیرا این سازه توسط چندین شاخص اندازه گیری شده است و ما این شاخص ها را توسط عملیات compute به یک ستون در نرم افزار spss تبدیل کرده ایم. بنابراین شرط اول برقرار است.
شرط دوم) جنسیت متغیری اسمی(کیفی) و دو ارزشی است بنابراین شرط دوم برقرار است.
شرط سوم) همچنین گروه های آقایان و خانم ها از یکدیگر مستقل هستند که منجر به تایید شرط سوم می شود
شرط چهارم) همچنین در بخش پیش پردازش ها شکل توزیع متغیر های پژوهش بررسی شده است که نشان می دهد توزیع داده های این متغیر ها نرمال هستند بنابراین پیش شرط چهارم برای انجام آزمون t با دو نمونه مستقل برقرار است( توجه شود که پیش تست نرمال بودن توزیع داده های سازه عوامل ایجاد کننده استرس باید حتما توسط آزمون چولگی و کشیدگی سنجیده شود. پیرامون این موضوع در مقالات گذشته و کتاب های قرار داده شده در سایت بحث های کاملی انجام شده است)
آدرس اجرای آزمون:
Analyze > Compare Mean > Independent-Sample T Test
بعد از اجرای دستور مطابق با شکل زیر متغیر هایی که قصد مقایسه ی آن ها را داریم را به پنجره ی Test variable(s) می بریم. همچنین متغیر جنسیت را به قسمت grouping variable می بریم و Define Groups را کلیک کرده و عدد 1 را در گروه 1 و عدد 2 را در گروه 2 وارد می کنیم و continue را می زنیم و در نهایت در پنجره اول ok را می زنیم.
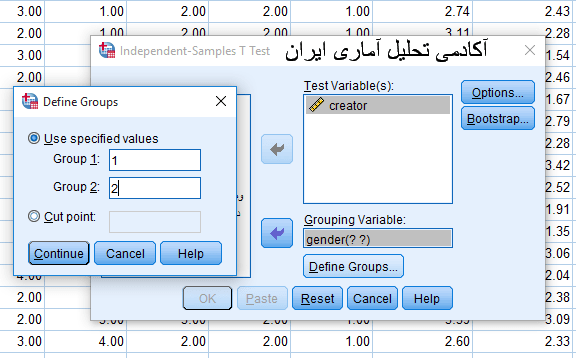
در پنجره خروجی دو جدول ظاهر می شود. جدول اول اطلاعاتی توصیفی از هر گروه مستقل مثل حجم نمونه هر گروه مستقل، میانگین، انحراف معیار و ….گزارش شده است. اما جدول دوم جدولی است که نتایج آزمون بر اساس آن تفسیر می شود.
این جدول شامل دو سطر است که ابتدا محقق باید درک کند کدام سطر باید برای تفسیر نتایج او استفاده گردد. همانطور که مشخص است سطر اول زمانی باید بررسی شود که واریانس های دو گروه آقا و خانم با هم برابر هستند و سطر دوم زمانی باید بررسی شود واریانس های دو گروه آقا و خانم با هم برابر نیستند. خوب این همان سوالی است که محقق از خود می پرسد که کدام سط را بخوانم؟
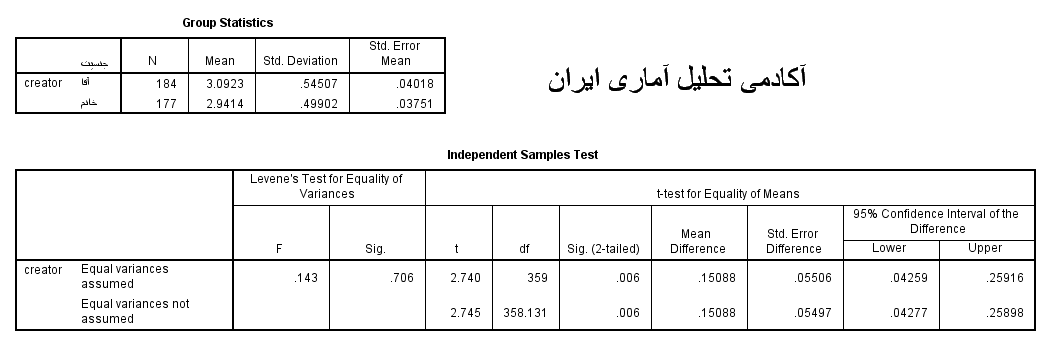
پاسخ به این سوال را آزمونی به نام آزمون لوین به شما خواهد داد. آزمون لوین آزمونی برای تشخیص برابری و عدم برابری واریانس ها است. یعنی فرض آماری آن به صورت زیر می باشد:
واریانس های دو گروه با هم برابر هستند H0:
واریانس های دو گروه با هم برابر نیستند H1:
با توجه به نتایج آزمون لوین مشخص است که سطح معناداری(sig) بالاتر از مقدار 0.05 است یعنی فرض H1 رد و فرض H0 پذیرفته می شود. بنابراین واریانس گروه های مستقل آقایان و خانم ها در سازه عوامل استرس زا (Creator) با هم برابر هستند. بنابراین در جدول زیر سطر اول هر سازه برای آزمون t که با پیش شرط برابری واریانس ها است، بررسی می شود.
فرضیه مبنی بر اینکه «متغیر سازه ایجاد کننده استرس در بین دانشجویان آقا و خانم تفاوت دارد» در نتیجه فرض آماری بصورت زیر تنظیم می شود.
H0: µ1= µ2
H1: µ1≠ µ2
با توجه به اطلاعات مندرج در جدول ، ميتوان دريافت که بر اساس مقدار sig که کمتر از 0.05 است در سطح اطمینان 99 درصد فرض H0 رد و فرض H1 تایید می شود. یعنی سازه عوامل ایجاد کننده استرس در بین دو گروه خانم ها و آقایان تفاوت دارد.
تا اینجای کار تنها تفاوت میانگین در بین دو گروه دانشجویان دختر و پسر مورد تایید قرار گرفته است و جهت آن یعنی اینکه کدام یک دارای میانگین بزرگتری برای این متغیر است، بحثی انجام نشده است.
در مورد جهت آن باید بیان کرد که:
- اگر حد بالا و پایین هر دو مثبت باشند در این صورت میانگین گروه اول از میانگین گروه دوم بزرگتر است.
- اگر حد بالا و پایین هر دو منفی باشند در این صورت میانگین گروه دوم از میانگین گروه اول بزرگتر است.
- اگر حد بالا و پایین یکی مثبت و یکی منفی باشند در این صورت میانگین های دو گروه با هم تفاوت معناداری ندارد.
در فرضیه بالا حد بالا و پایین هر دو مثبت هستند بنابراین میانگین گروه اول یعنی آقایان بزرگتر از میانگین گروه دوم یعنی خانم ها است و تایید شد که این اختلاف از نظر آماری معنادار است.
مقالات بعدی مرتبط:
آزمون F تحلیل واریانس یک طرفه یا ANOVA
تحلیل واریانس چند متغیره یا Manova
دکتر محسن مرادی
دکتر آیدا میرالماسی
دیدن دوره رایگان زیر را به همه محققان پیشنهاد می کنیم
فیلم آموزش تصویری سرچ با استراتژی علمی به همراه آموزش publish or perish
مطالب سایت و کانال انحصارا توسط این سایت تولید می شود و از استفاده آن بدون ذکر منبع سایت خودداری شود
 مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران
مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران



سلام ممنون از مطالب خوبتون.
ببخشید در آخر بحث نوشته شده میانگین گروه اول یعنی آقایان بزرگتر از میانگین گروه دوم یعنی خانم ها است. این یعنی چی؟ یعنی پاسخی ک مردان دادن بیشتر از زنان بوده؟ یا مردان پاسخهایی کاملا موافق بیشتری ب سوالات دادند؟
ببینید آزمون تی دو نمونه مستقل قرار نیست مقایسه ای با یک استاندارد انجام بده بلکه یک میانگین یک متغیر در جامعه بین دو گروه مستقل از هم مقایسه می شود. مثلا فرض کنید در انتهای آزمون مشخص بشه میانگین متغیر رضایت در آقایان از خانم ها بیشتر است. این یعنی آقایان در آن متغیر از سطح میانگین بزرگتری برخوردار هستند. یعنی آقایان از خانم ها رضایت بالاتری دارند.بنابراین مورد دوم که بیان کردید درستتر است
خیلی ممنونمممم
سلام
تعداد نمونه در هر گروه آزمایشی و گروه گواه، چقدر باید باشه که بتونیم از آزمون t استفاده کنیم؟
استاد گرامي بابت همه زحمات و آموزش هايتان سپاسگزارم
خدا قوت بسیار عالی
واقعا این مطلبتون به من کمک زیادی کرد. ممنون ازتون
با سلام و خسته نباشید.
اگر بخواهیم از مطالب شما ارجاع بدیم در مقالاتمون. آقای دکتر مرادی و خانم دکتر کتابی چاپ شده یا در حال چاپ دارن؟
بله عزیم اطلاعات کتاب شناسی رو براتون میزاریم. تو مطلب آخرم هست اگه نگاه کنید
واقعا ممنون خیلی توضیحاتتون کاربردی بود
بسیار عالی و مفید
تشکر فراوان
سلام
ببخشید من برای درس سمینار احتیاج به مطالبی راجع به تی دو نمونه مستقل دارم ,میشه اطلاعات بیشتری در این مورد در اختیارم بذارید یا کتابی معرفی کنید ؟
عزیزم. متاسفانه کتاب های فارسی ضعیف هستند. اما بدون برای درک این مفاهیم هم روش تحقیق هم آمار کاربردی و هم نرم افزار رو باید یاد گرفت و این مطلب در حقیقت یه آزمون کوچک از یک کلاس 50 ساعته SPSS این موسسه بوده و واقعا الان اگه کتابی هم بهت معرفی کنم تنها بخش نرم افزار را پوشش میده که من اون بخش رو کامل تر همینجا اوردم
خيلي خوب بود
سلام
وقت بخیر
من از این مطالب برای تحقیق خودم استفاده کردم ممنون میشم رفرنس موردنظررا بفرمایید
مرادی, م., & میرالماسی, آ. (1398). روش پژوهش عملگرا.، آکادمی تحلیل آماری ایران(Ed مدرسه پژوهش کمی و کیفی,) (اول). تهران. Retrieved from http://www.analysisacademy.com
سلام ببخشید ازمون تی تست دو گروه با واریانس مشترک برای چی استفاده میشه؟
سلام عزیزم. برای مقایسه یک متغیر در دو گروه. مثلا مقایسه استرس بین دو گروه خانم و آقایانو البته واریانس مشترک نداریم. یا واراینس برابره یا نابرابره مه در مطالب بیان شده
سلام وقت بخیر در صورت برابر نبودن واریانس ها در ازمون لونز، اونوقت چه اتفاقی میوفته؟
سلام عزیزم خوب دو خط خروجی می دهد. هم با شرط برابری واریانس و هم شرط عدم برابری. شما باید خط دوم را به عنوان پاسخ نتایج خود در نظر بگیرید
سلام
در صورتی که هدف مقایسه دو گروه زن و مرد است باید نرمال بودن برای هر گروه محاسبه شود؟
سلام عزیزم سوالی که پرسیدی در کلاس ها به عنوان یکی از مشکلات بزرگ تحقیقات ایران گفته شده است. کافی در مقالات 2020 به بعد پیرامون آزمون نرمال بودن سرچ کنید. نکته دوم در مورد سوال شما این است متغیر اسمی مثل جنسیت که آزمون نرمال بودن براش معنی ندارد. آزمون نرمالیته باید روی متغیری که قرار است بین این دو گروه مقایسه شود انجام می شود. اون متغیر هم چون دارای طیف لیکرت است باید آزمون چولگی و کشیدگی زده شود. اما اگر یک متغیر ذاتا کمی مثل قد، درآمد و …. قرار بر مقایسه باشد آزمون نرمالیته بنا بر شرایط آموزش داده شده در کلاس ها که الان مجال بیان آن نیست، توسط آزمون هایی مثل شاپیرو، کلموگروف و اسمیرنف تک نمونه ای، دی آگوستینو و … اجرا می شود.
و این که چرا برای بررسی نرمال بودن متغیر در دو مستقل باید چولگی و کشیدگی را بررسی کرد نه سایر آزمون ها را؟
با سلام و عرض ادب
آیا می شود در یک پژوهش دو جامعه متفاوت داشت و دو متغیر متفاوت و بعد بین آن ها رابطه و یا تاثیر را اندازه گیری کرد.مثلا متغیر های وفاداری مشتری و ارزش ادراک شده برند در مشتری ها و رابطه و یا تاثیر آنها با تعهد اجتماعی مدیران تولید کننده برند یا کالا و بنابراین پرسشنامه ها و داده ها در دو گروه جدا جمع آوری شوند؟ یک گروه مشتریان و گروه دیگر تولید کنندگان؟ متشکرم
سلام. عزیزم اینو در کلاس ها توضیح دادم و مثال آوردم. اگر نبودی جواب بله. باید از روش پکیجینگ استفاده کرد
من تو کلاس چهار جامعه ای رو مثال زدم. مربوط به مقاله از ترکیه در سال 2016 با عنوان service oriented………. بود. با این کلید واژه بگرد پیداش می کنی
با سلام و وقت بخیر
در مورد مقایسه وضعیت تاهل در یک متغیر که با روش تی مستقل آزمون می شود کدام فرضیه صحیح است؟
بین وضعیت تاهل دانشجویان و رفتار پرخطر جنسی رابطه وجود دارد
یا
بین رفتار پرخطر در دانشجویان مجرد و متاهل تفاوت وجود دارد
با تشکر از شما
سلام
سازه رفتار پر خطر در بین دانشجویان مجرد و متاهل تفاوت دارد