تحلیل واریانس چند متغیره یا Manova

تحلیل واریانس چند متغیره یا Manova

با توجه به تقاضای بسیاری از محققین عزیز بر آن شدم که یکی از پیچیده ترین آزمون های آماری یعنی آزمون تحلیل واریانس چند متغیره  MANOVA را در این مقاله مورد بحث قرار دهیم و تلاش کنیم که به زبان ساده آن را باز کرده و مفاهیم، نحوه اجرای آن در نرم افزار و از همه مهمتر تفسیر نتایج مهم آن را به عزیزانم آموزش دهیم.

نکته ی اولی که بیان می کنم این است که عزیزان حتما پیش از مطالعه این مقاله به مقاله آزمون F تحلیل واریانس یک طرفه یا ANOVA رجوع نمایند و با دقت آن را مطالعه کنند زیرا در غیر این صورت جان مطلب این مقاله را دریافت نخواهند کرد یا لااقل کاملا دریافت نخواهند کرد. در آن مقاله بیان شد که تحلیل واریانس یک طرفه   ANOVA   برای آزمون مقایسه میانگین یک متغیر کمی در بین بیش از دو گروه مستقل استفاده می شود. در حقیقت این آزمون تعمیم یافته همان آزمون T دو نمونه مستقل است و دارای همان پیش فرض ها می باشد و تنها تفاوت این است که میانگین متغیر های کمی در بیش از دو گروه مستقل با هم مقایسه می شوند(مرادی، ۱۳۹۵).

در آزمون MANOVA باید ذکر نمایم که اگر زمانی قصد داشتیم بجای مقایسه میانگین یک متغیر کمی، بیاییم و میانگین بیش از یک متغیر کمی را در بین بیش از دو گروه مستقل مقایسه نماییم می توانیم از MANOVA یا تحلیل واریانس چند متغیره استفاده نماییم. یعنی در حقیقت این آزمون تعمیم یافته آزمون ANOVA است.

ابتدا به دقت پیش فرض های این آزمون را بررسی نماییم.

1. اولا وقتی بیان می شود ما می توانیم میانگین چند متغیر کمی(SCALE) را در گروه ها مقایسه کنیم عمدتا این چند متغیر مولفه های یک سازه اصلی هستند. مثلا به فرضیه ی زیر دقت کنید:

تعهد سازمانی در بین کارکنان بخش مالی، بازاریابی و تولید با تحصیلات مختلف تفاوت دارد.

خوب اولا این فرضیه و آزمون MANOVA همانطور که در کلاس های آکادمی تحلیل آماری ایران بیان شد، فرضیه ای تفاوتی است. این نکته را برای آن ذکر کردم که بعضا دانشجویانی سوال می کنند من فرضیه ای به این شکل دارم آیا باید از روش های رگرسیونی(مدل سازی معادلات ساختاری استفاده کنم). فرضیه آن ها بدین صورت است:

تحصیلات کارکنان بخش های مالی، بازاریابی و تولید بر تعهد سازمانی تاثیر می گذارد.

بعد بیان می کنند که چون کلمه تاثیر در فرضیه آمده پس فرضیه علی است و باید از تجزیه و تحلیل فرضیات علی را بکار برد. در صورتی که با کمب دقت مشخص است که فرضیه بدین صورت است که قرار است به مقایسه میانگین تعهد سازمانی در گروه های مالی، بازاریابی و تولید و نیز در گروه های لیسانس، فوق لیسانس و دکتری پرداخت. همانطور که میبینیم در این آزمون حداقل باید دو متغیر کیفی(کارکنان بخش ها، تحصیلات) که اسمی یا رتبه ای هستند برای اینکه مقایسه میانگین در آن ها انجام شود وجود داشته باشد.

از طرفی همانطور که اول پیش فرض بیان شد یکی از مهمترین موضوعات این است که وقتی بیان می کنیم چند متغیر کمی در این متغیر ها کیفی مورد مقایسه میانگین قرار می گیرند، این چند متغیر خود مولفه های یک سازه هستند. در فرضیه ما نیز این گونه است.(مرادی، 1395)

یعنی تعهد سازمانی خود شامل سه مولفه یا خرده مقیاس:

1)تعهد عاطفی

2)تعهد هنجاری

3)تعهد مستمر

است. یعنی در این آزمون همزمان میانگین متغیرهای کمی تعهد عاطفی و تعهد هنجاری و تعهد مستمر در دو متغیر کیفی(کارکنان بخش ها، تحصیلات) که یکی اسمی و دیگری ترتیبی است مقایسه می شوند.

2. پیش فرض دوم این است که این متغیر های کمی دارای توزیع نرمال باشند ( توجه شود که پیش تست نرمال بودن توزیع داده های متغیرهای کمی تعهد عاطفی ،  تعهد هنجاری و تعهد مستمر باید حتما توسط آزمون چولگی و کشیدگی سنجیده شود. پیرامون این موضوع در مقالات گذشته و کتاب های قرار داده شده در سایت بحث های کاملی انجام شده است).
3. متغیر هایی که در گروه های مستقل آن ها مقایسه انجام می شود باید در سطح سنجش اسمی یا رتبه ای باشند. یعنی کیفی باشند.
4. مقایسه میانگین متغیر های کمی باید در بیش از یک متغیر کیفی انجام شود. اگر در آزمون ANOVA به خاطر داشته باشد مقایسه میانگین در یک متغیر کیفی با چند گروه مستقل انجام می شد. اما در این آزمون همانطور که می بینید بیش از یک متغیر کیفی داریم و همزمان میانگین متغیرهای کمی تعهد عاطفی، تعهد هنجاری و تعهد مستمر در دو متغیر کیفی(کارکنان بخش ها، تحصیلات) که یکی اسمی و دیگری ترتیبی است مقایسه می شوند. این متغیر های کیفی در نرم افزار SPSS عامل یا FACTOR خوانده می شود.

بعد از بیان پیش فرض ها باید بیان کنیم که گاه محققین سوال می کنند که چرا بجای استفاده از MANOVA که آزمون دشواری می باشد، به طور جداگانه چند بار از تحلیل واریانس یک طرفه یا ANOVA برای یک یک متغیرها نمی کنیم. جواب دوستان در این است که آزمون MANOVA دو کار اصلی را انجام می دهد:

1. یکی از وظایف این آزمون این است که درست مثل ANOVA هر متغیر کمی(هر یک از مولفه های تعهد سازمانی) را بطور جداگانه در هر یک از گروه های متغیر های کیفی مقایسه میانگین کند.
2. اما وظیفه اصلی این آزمون این است که بطور همزمان بیان کند که کل این سه مولفه که مجموعا سازه تعهد سازمانی را می سازند بصورت یکجا آیا در بین گروه های مستقل متغیر های کیفی تفاوت میانگین دارد یا خیر؟  این سوال پاسخی می خواهد که توان آن را آزمون ANOVA ندارد.بنابراین پاسخ به فرضیات اصلی که در ذیل آورده شده وظیفه اصلی آزمون MANOVA است.

پس در این آزمون این فرضیات تست می شود:

• تعهد سازمانی در بین کارکنان مالی، بازاریابی و تولید شرکت تفاوت دارد.(فرضیه اصلی)
• تعهد سازمانی در بین کارکنان لیسانس، فوق لیسانس و دکتری بخش های سه گانه شرکت تفاوت دارد.(فرضیه اصلی)
• تعهد عاطفی در بین کارکنان مالی، بازاریابی و تولید شرکت تفاوت دارد.
• تعهد عاطفی در بین کارکنان لیسانس، فوق لیسانس و دکتری بخش های سه گانه شرکت تفاوت دارد.
• تعهد هنجاری در بین کارکنان مالی، بازاریابی و تولید شرکت تفاوت دارد.
• تعهد هنجاری در بین کارکنان لیسانس، فوق لیسانس و دکتری بخش های سه گانه شرکت تفاوت دارد.
• تعهد مستمر در بین کارکنان مالی، بازاریابی و تولید شرکت تفاوت دارد.
• تعهد مستمر در بین کارکنان لیسانس، فوق لیسانس و دکتری بخش های سه گانه شرکت تفاوت دارد.

همانطور که در شکل زیر می بینید داده های سه مولفه ی کمی تعهد سازمانی و دو متغیر کیفی کارکنان بخش ها و تحصیلات کارکنان در فایل SPSS وارد شده است. نحوه اجرای دستور آزمون MANOVA در نرم افزار SPSS به صورت زیر است:

Analyze > General Linear Model > Multivariate…

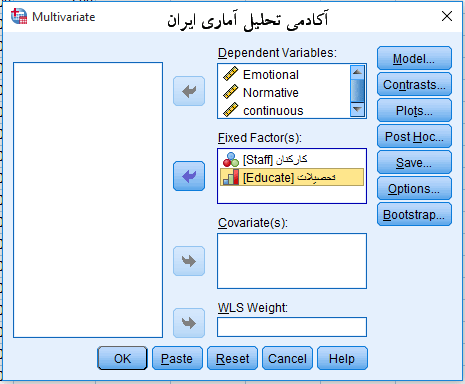
حال در پنجره دیالوگ باز شده سه مولفه کمی تعهد عاطفی، هنجاری و مستمر را به پنجره Dependent Variables منتقل کنید. پس از آن دو متغیر کیفی کارکنان بخش ها و تحصیلات را به پنجره ی Fixed Factors منتقل می کنیم.

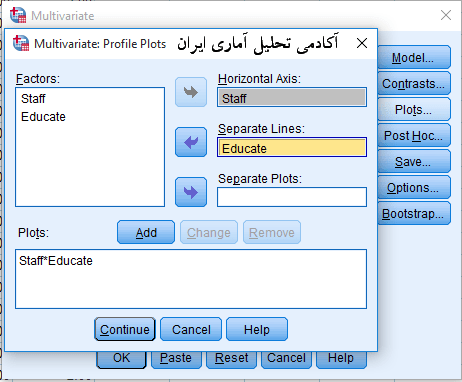
سپس دکمه Plots را زده و عامل کیفی کارکنان بخش ها را در کادر Horizontal Axis و بعد تحصیلات را به عنوان عامل دوم در کادر Separate Lines وارد می کنیم و کلید Add را می زنیم تا حاصلضرب دو عامل در کادر زیرش به عنوان حاصلضرب دو عامل ظاهر شود. سپس کلید continue میزنیم.

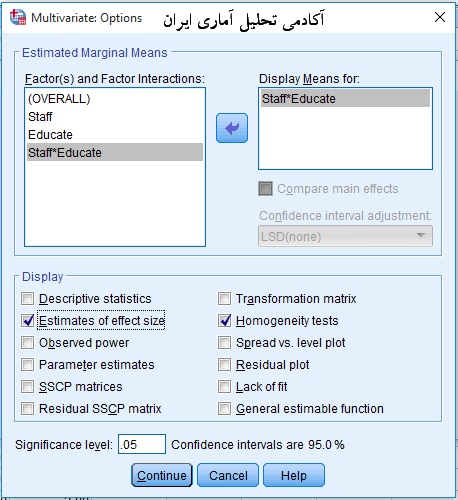
بعد دکمه optionsرا در پنجره دیالوگ اصلی زده و حاصلضرب دو عامل را به سمت راست می بریم و در قسمت Display  تیک آزمون Homogeneity tests و Estimates of effect size را می زنیم. سپس کلید continue میزنیم. و بعد ok زده و آزمون را اجرا می کنیم.

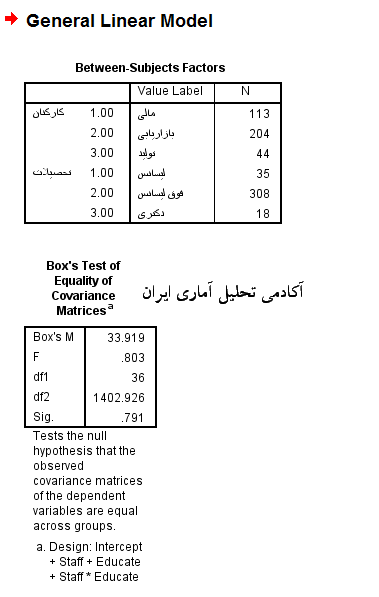
حال باید به سراغ تفسیر خروجی های آزمون رفت. همانطور که در اولین جدول خروجی مشاهده می شود تعداد پاسخ گویان در هر عامل( متغیر کیفی) نشان داده می شود.

اما یکی از مهمترین خروجی های این آزمون، آزمون جدیدی است که به شما عزیزان معرفی می شود. آزمونی که قرار است مورد بحث قرار گیرد آزمون ام باکس BOX,S M است. ابتدا ببینیم این آزمون چیست و چرا از آن استفاده می شود.

باید در نظر داشت که متغیر های کمی این پژوهش که در حقیقت ابعاد سه گانه سازه تعهد سازمانی هستند با یکدیگر  در گروه های مختلف هر متغیر کیفی این تحقیق همبستگس(رابطه) دارند. یعنی مثلا در متغیر کیفی تحصیلات که شامل سه گروه مستقل است هر یک از ابعاد سه گانه تعهد سازمانی دارای کوارانس یا (در حالت استاندارد همبستگی) هستند. این الگوهای همبستگی بین ابعاد تعهد سازمانی در ماتریس های واریانس – کواریانس بررسی می شود که از این پس به اختصار آن ها را ماتریس های کواریانس بین ابعاد تعهد سازمانی می نامیم.

حال این نکته را باید بیان کرد که یکی از پیش فرض های مهم آزمون تحلیل واریانس چند متغیره این است که ماتریس های کواریانس در هر یک از گروه های متغیر های کیفی (مثلا تحصیلات) باید همگن باشد. تشخیص همگن بودن این ماتریس های کواریانس را آزمون ام باکس انجام می دهد. این آزمون را برای متغیر های کیفی به صورت زیر می نویسیم.

H0: ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان مالی

=ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان بازاریابی

= ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان تولید

H1: ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان مالی

≠ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان بازاریابی

≠ ماتریس کواریانس بین مولفه های تعهد سازمانی در بین کارکنان تولید

این فرض های آماری عینا برای سه گروه متغیر کیفی تحصیلات نیز نوشته می شود. اما نکته اینجاست که بر خلاف همیشه در این فرض های آماری محقق  دوست دارد که فرض  H0 که صحبت از همگن بودن ماتریس های کواریانس متغیر های کمی می کند، معنادار شود و مورد تایید قرار گیرد. در بتوان در مراحل بعدی از آزمون های قدرتمند تری برای تحلیل نتایج استفاده نمود. خوب حال که به جدول بالا که آزمون ام باکس در آن انجام شده نگاه می کنیم، مشاهده می شود که مقدار خطایی که محقق در این آزمون مرتکب می شود یعنی sig بیشتر از 0.05 درصد بوده است بنابراین فرض صفر پذیرفته می شود و این بدان معناست که ما شاهد برابری ماتریس های کواریانس مشاهده شده متغیر های کمی تحقیق( یعنی مولفه های تعهد سازمانی) در بین گروه های مستقل مختلف هر یک از عامل ها هستیم.

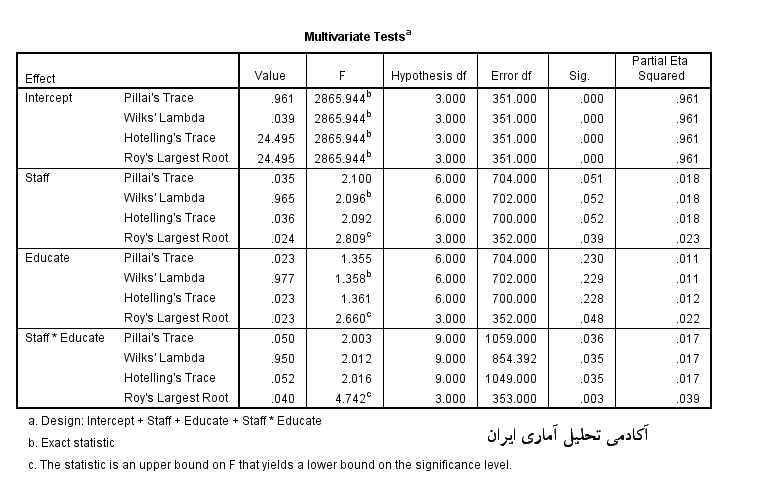
حال به سراغ مهمترین جدول خروجی این آزمون می رویم. همانطور که در این جدول (جدول زیر) می بینیم ابتدا باید با 4 آزمون مهم در آن آشنا شویم تا بتوانیم تفسیر درستی از نتایج داشته باشیم.

1. اولین آزمون را آزمون اثر پیلای می خوانند.

2. آزمون دوم را لاندای ویلک می خوانند که در برخی از ادبیات آماری به آن آزمون u نیز می گویند. این آزمون بین صفر و یک نوسان دارد و هر چه به مقدار صفر نزدیک شود گواهی به تفاوت بیشتر میانگین متغیر های کمی در گروه ها می دهد و بر عکس هر چه به یک نزدیکتر نشان از عدم تفاوت میانگین ها در بین گروه ها است.

3. آزمون سوم اثر هتلینگ نام دارد که مقادیر ارزش ویژه و مجموع آن برای آن محاسبه می شود.

4. در نهایت آزمون چهارم را بزرگترین ریشه روی می نامند.(مرادی، 1395)

در بین آزمون های بالا آزمون لاندای ویلک از بقیه رایج تر و پر کاربرد تر بوده است اما آزمون اثر پیلای از بقیه بسیار قدرتمند تر است با این پیش شرط که ماتریس های کواریانس همگن باشد که خوشبختانه در این مثال این شرط براورده شد

اما اینکه این آزمون ها چه می گویند باید بیان کرد که همان وظیفه اصلی آزمون manova را انجام می دهند. یعنی ما در اول بحث بیان کردیم که چرا بجای استفاده از این آزمون، چند بار از آزمون anova استفاده نمی کنیم؟ پاسخ این است که آژمون anova به بررسی تفاوت میانگین یک متغیر کمی در گروه های یک متغیر کیفی می پردازد، اما اکنون  این متغیر های کمی همگی ابعاد یک سازه اصلی به نام تعهد سازمانی هستند و محقق برای اینکه به صورت کلی بیان کند که خود سازه تعهد سازمانی در بین گروه های مستقل از نظر میانگین چه تفاوتی دارد چاره ای ندارد جز استفاده از آژمون واریانس چند متغیره یا manova.

جدول Multivariate tests دقیقا به همین سوال اصلی پاسخ می دهد. اگر به بخش staff نگاه کنید و مقدار sig را مشاهده کنید سازه تعهد سازمانی در گروه های مختلف کارمندان برای 3 آزمون از 4 آزمون اصلی معناداری نیست یعنی میانگین سازه تعهد سازمانی در بین گروه های مختلف کارکنان تفاوت معناداری ندارد. این نتیجه برای گروه های متغیر دوم کیفی، تحصیلات نیز دوباره تکرار شده است. البته محققین می توانند به آزمون ریشه روی که آزمون چهارم است استناد کنند و بگویند در این آزمون مشخص شده که تفاوت میانگین ها معنادار است. اما این آزمون نسبت به بقیه آزمون ها لیبرال تر بوده و سخت گیرانه عمل نمی کند( قبلا در کلاس های آکادمی تحلیل آماری پیرامون این مفاهیم بحث شده است)

اما مهمترین نتیجه مربوط به تفاوت میانگین ها در بین اثر متقابل گروه های کارمندان و تحصیلات آن ها است. یعنی staff*educate.

مشخص است که مقدار sig در هر 4 آزمون در این بخش کوچکتر از 0.05 است. بنابراین تفاوت میانگین تعهد سازمانی بر اساس هر 4 آزمون در سطح اطمینان 95 درصد مورد تایید قرار می گیرد. یعنی سازه تعهد سازمانی در گروه های مختلف تحصیلی بخش های مالی، بازاریابی و تولید تفاوت دارد. یا به صورت دیگر می توان گفت که تحصیلات بخش های مختلف مالی، بازاریابی و تولید بر تعهد سازمانی کارکنان تاثیر می گذارد.

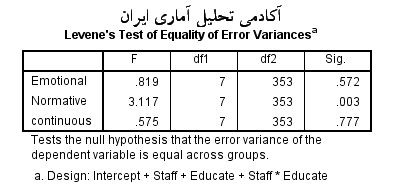
در بخش دیگر تفسیر ها به سراغ آزمون لوین می رویم. آزمون لوین در ایجا آزمونی برای تشخیص برابری و عدم برابری واریانس ها خطاها است. یعنی فرض آماری آن به صورت زیر می باشد:

واریانس های خطاهای گروه ها با هم برابر هستند:H₀ 

واریانس های خطاهای گروه ها با هم برابر نیستند :H₁

 با نگاهی به نتایج جدول لوین مشخص است که مقدار sig برای دو مولفه تعهد عاطفی و مستمر بالای 0.05 است بنابراین واریانس های خطا های آن ها با هم برابر هستند همچنین مقدار sig برای مولفه تعهد هنجاری پایین 0.05 است بنابراین واریانس خطاهای آن ها در گروه های مختلف با هم برابر نیستند.

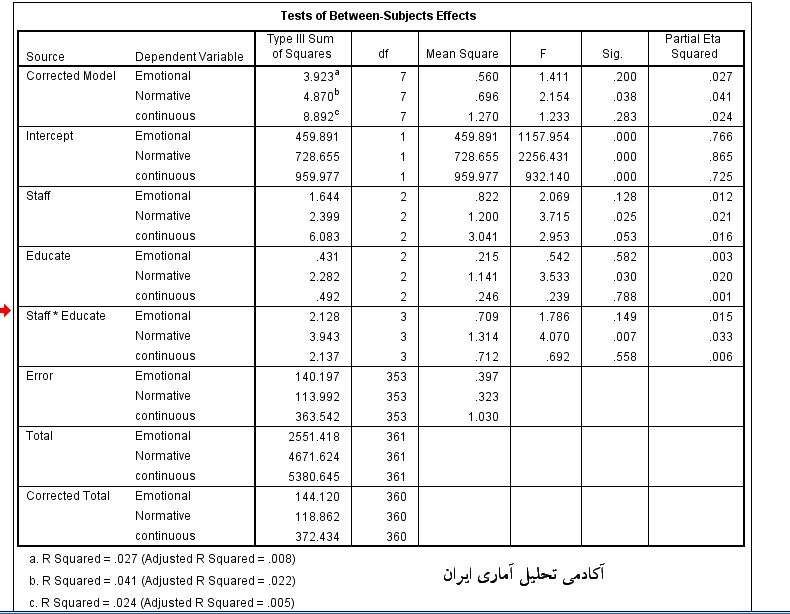
در جدول بعدی یعنی جدول Test of Between-Subjects Effects به بررسی اثرات هر یک از متغیر های کمی(مولفه های تعهد سازمانی) به صورت جداگانه در گروه های متغیر های کیفی و نیز اثر تعاملی آن دو متغیر می پردازد.

 سه بخش staff و educate  و حاصلضرب آن ها اطلاعات اصلی را منتقل می کند. با توجه به مقدار sig در هر سه بخش تنها تفاوت میانگین مولفه تعهد هنجاری از نظر آماری معنادار است زیرا مقدار sig کمتر از 0.05 است. یعنی هم در کارمندان بخش های مختلف، هم در تحصیلات مختلف و هم اثر تعاملی آن ها میانگین دو مولفه ی تعهد عاطفی و تعهد مستمر تفاوت معناداری ندارد.

در اینجا درست مثل آزمون anova باید بیان کرد برای آنکه تشخیص دهیم این تفاوت بین کدام گروه ها است میتوان از آزمون های تعقیبی یا post hoc استفاده کرد. این بحث را قبلا در مقاله آزمون F تحلیل واریانس یک طرفه یا ANOVA به طور کامل آموزش دادیم. از طرفی ستون آخر جدول بالا درصد واریانس تبیین شده از متغیر های کمی، یعنی مولفه های تعهد سازمانی توسط متغیر های کیفی گزارش شده است.

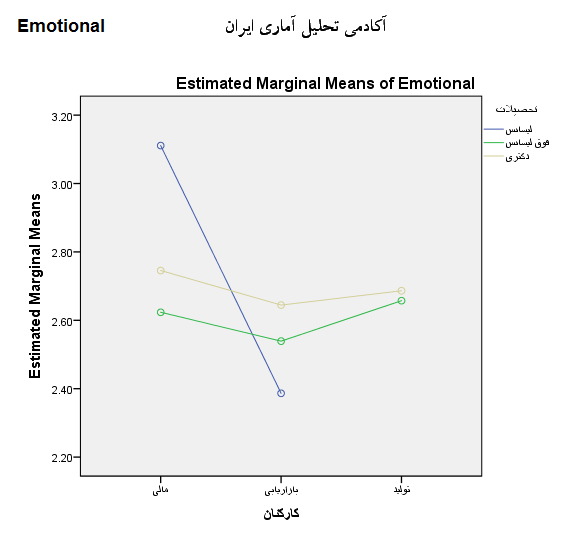
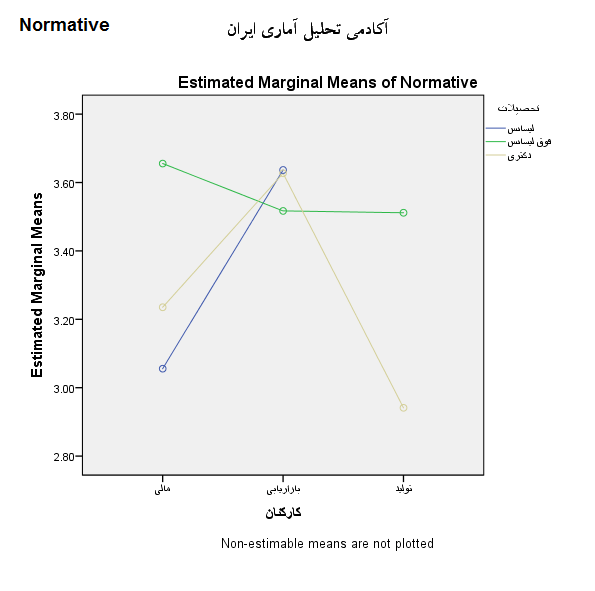
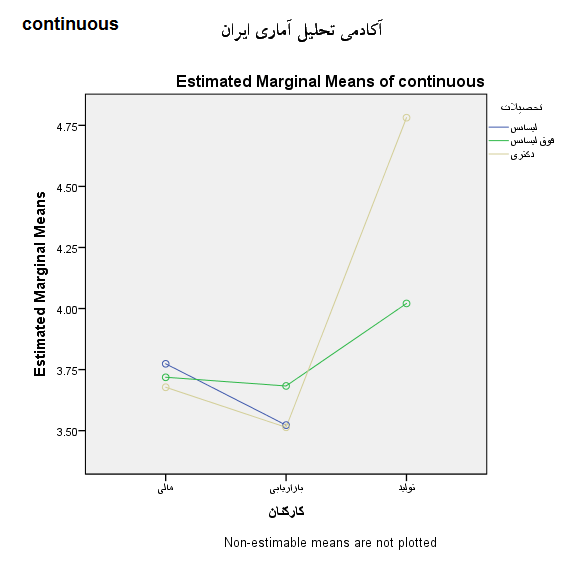
در بخش آخر تفسیر نمودارهای گرافیکی نیز آورده شده است. هر چه خطوط این نمودارها موازی تر باشند یعنی میتوانیم قضاوت کنیم که تعمل کمی بین عامل ها وجود دارد.(مرادی، 1395)

تالیف و نگارش: محسن مرادی

فیلم آموزش تصویری سرچ با استراتژی علمی به همراه آموزش publish or perish

مطالب این سایت توسط اعضای تحریریه این سایت تولید شده لذا از کپی برداری و استفاده در جای دیگر خودداری شود.