مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران
حجم نمونه در نمونه گیری طبقه ای
در مطالب قبلی بیان شد که در نمونه گیری تصادفی ساده برای هر یک از واحد ها شانس و احتمال برابر در نظر می گیرند. این بدان دلیل است که اطلاعی از واحد های جامعه در دست نیست ولی اگر اطلاع داشته باشیم که تفاوت بین واحد ها خیلی زیاد است در این صورت مشخص کننده های آماری جامعه با استفاده از روش نمونه گیری تصادفی ساده ناتور بوده و برآورد صحیح از آن بدست نخواهد آمد.
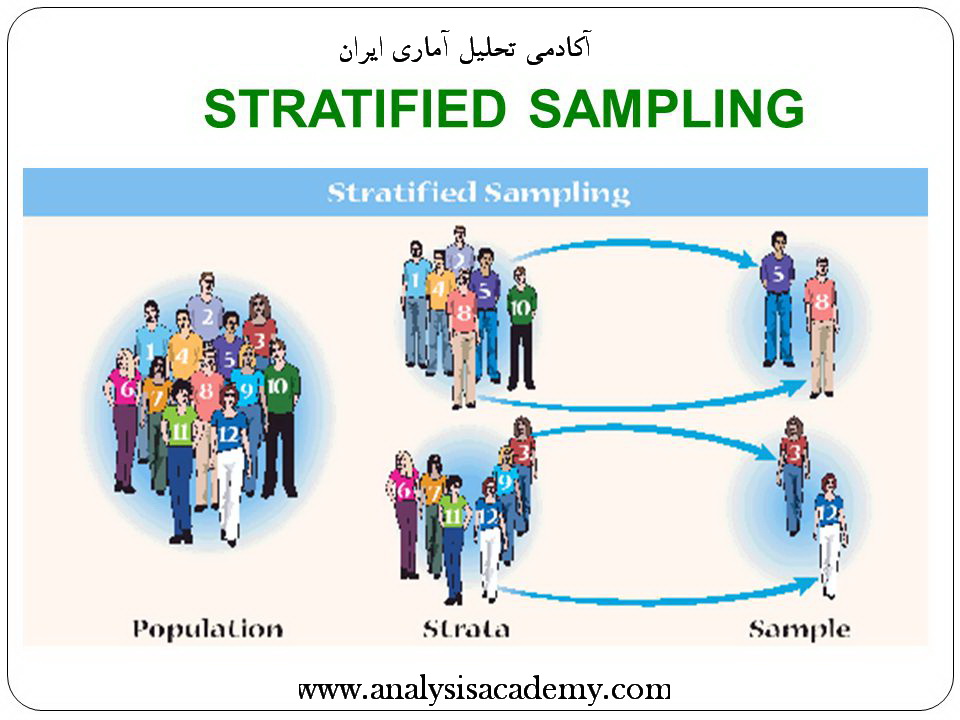
در این حالت در نمونه گیری تصادفی از طبقه بندی جامعه به جامعه های جزء استفاده می شود. به سخن دیگر اگر واریانس بین طبقات زیاد و درون طبقات کم باشد در این صورت جامعه را طبقه بندی می کنند. برای آنکه نمونه انتخاب شده از همه واحد های جامعه تعدادی را شامل باشد در داخل هر طبقه نمونه گیری مستقل انجام می گیرد، یعنی در داخل هر جامعه جزئی که در این مقام خود یک طبقه (Stratum) نامیده می شود با همان اصول مربوط به انتخاب تصادفی تعدادی از واحد ها را به عنوان نمونه انتخاب می نمایند. امتیاز نمونه گیری طبقه بندی در آن است که می توان واحد های جامعه را به شکلی طبقه بندی کرد که اولا هزینه تحقیق کم شود و ثانیا به علت کم بودن واریانس طبقات دقت آمار گیری بیشتر گردد.
در نمونه گیری طبقه بندی تعداد نمونه هر طبقه رایا از روش انتساب اپتیموم بدست می آورند و یا اینکه متناسب با بزرگی انتخاب می کنند. در روش انتساب اپتیموم برای دقت معین، حجم نمونه لازم برای کل جامعه به حداقل می رسد. بنابراین مخارج نمونه گیری کمتر از روش انتساب متناسب با حجم می باشد. در نتیجه روش انتساب اپتیموم به روش انتساب متناسب بر حجم برتری دارد.
حجم نمونه در هر طبقه با استفاده از روش متناسب از فرمول:
ni = (Ni / ∑Ni) n
و استفاده از روش انتساب اپتیموم از فرمول زیر محاسبه می گردد.
ni = (NiSi / ∑NiSi) n
ملاحظه می شود که در روش انتساب متناسب فرض بر این است که واریانس طبقات یکسان می باشند.
محسن مرادی
از کپی کردن مطالب سایت و کانال بدون ذکر منبع خود داری شود.
