مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران
آزمون هم خطی
اکثر افرادی که در دوره های آکادمی تحلیل آماری ایران شرکت می کنند همواره سوالات زیادی راجع به آزمون هم خطی و شیوه اجرا و تفسیر آن دارند لذا در این بخش به توضیحاتی راجع به چگونگی اجرای آزمون هم خطی و نحوه تفسیر آن می پردازیم:
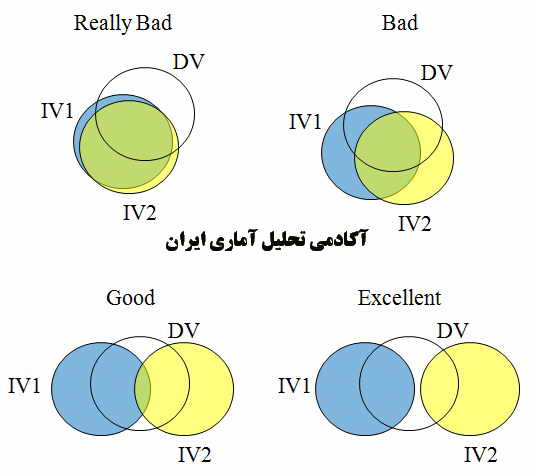
یکی از مفروضات مهم اکثر آزمونها به خصوص در آزمون های مربوط به فرضیه های علی این است که نباید بین متغییرها رابطه هم خطی وجود داشته باشد. بدین معنی که هیچ یک از متغییرهای مستقل نباید رابطه خطی با همدیگر داشته باشند. رابطه هم خطی وضعیتی است که نشان می دهد یک متغییر مستقل تابع خطی از سایر متغییرهای مستقل است. اگر هم خطی در یک معادله رگرسیون بالا باشد، بدین معنی است که بین متغییرهای مستقل همبستگی بالایی وجود دارد و در چنین حالتی با وجود بالا بودن R2 مدل اعتبار بالایی ندارد. به عبارت دیگر با وجود آنکه مدل خوب به نظر می رسد ولی دارای متغییرهای مستق معنی داری نمی باشد.
برای تشخیص هم خطی متغییرهای مستقل باید هنگام محاسبه رگرسیون غیر از برآورد model fit و Estimate،collinearity diagnostic را نیز انتخاب کنیم ؛ با این شیوه در جدولی شاهد نتایج آزمونهای تولرانس و عامل تورم واریانس نیز هستیم. تولرانس نسبتی از واریانس یک متغییر مستقل است که توسط سایر متغییرهای مستقل تبیین نشده است. ضریب تولرانس که بین صفر و یک نوسان دارد،نشان می دهد که متغییرهای مستقل تا چه اندازه رابطه هم خطی با همدیگر دارند. بنابراین هرچه مقدار تولرانس بیشتر نزدیک به عدد 1 باشد، میزان هم خطی کمتر است و برعکس هر چه مقدار تولرانس کم تر(نزدیک تر به عدد 0) باشد، نشان می دهد که میزان هم خطی بالاست و خطای استاندارد ضرایب رگرسیونی از تورم بالایی برخوردار خواهد بود.بنابراین در هنگام اجرای رگرسیون با مشکلاتی مواجه هستیم.
شاخص دیگر عامل تورم واریانس یا VIF است که از تقسیم عدد یک بر تولرانس حاصل می شود ، هرچه مقدار عامل تورم واریانس از عدد 2 بزرگ تر باشد میزان هم خطی بیش تر است. نتیجه و تفسیر عامل تورم واریانس، معکوس تولرانس است یعنی هر چه مقدار تولرانس بیش تر باشد، مقدار عامل نورم واریانس کم تر است و بر عکس. به عبارتی هر چه مقدار این ضریب افزایش یابد باعث می شود که واریانس ضرایب رگرسیونی افزایش یافته و در نتیجه مدل رگرسیون را برای پیش بینی نامناسب جلوه می دهد. بنابراین هر چه مقدار عمل تورم واریانس برای یک متغییر مستقل بیش تر باشد نتیجه می گیریم که که آن متغییر نقش زیادی در مدل ، نسبت به بقیه متغییرها ندارد.
