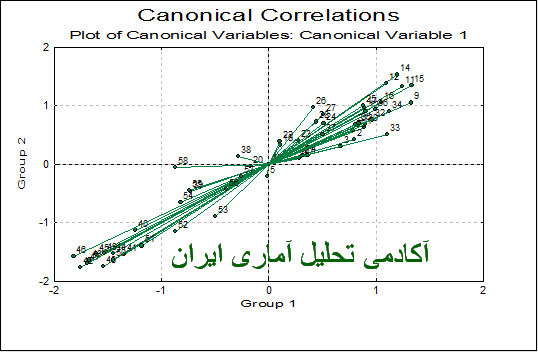
همبستگی کانونی(همبستگی بنیادی)

همبستگی کانونی(همبستگی بنیادی)

تاکنون در کلاس‌های آکادمی تحلیل آماری ایران با انواع ضرایب همبستگی مثل وی کرامرز و دی سامرز و کاپای کوهن و ….. که متأسفانه در فضای علمی و پژوهشی کشور کمتر استفاده می‌شود آشنا شده ایم و بیان کردیم هنگامی‌که دو متغیر با انواع سطح سنجش nominal  و ordinal و scale داریم چگونه می‌توانیم رابطه و همبستگی بین آن‌ها را بررسی نماییم. اما در بسیاری از مواقع متغیرها خود شامل مؤلفه‌های چندگانه هستند. مثلاً تعهد سازمانی خود شامل سه مؤلفه‌ی تعهد عاطفی و تعهد مستمر و تعهد هنجاری است. حال اگر بخواهیم رابطه‌ی این سازه را با سازه‌های دیگری که خود دارای مؤلفه‌های مختلف هستند چه راهکاری را باید در پیش گیریم. و یا با تحقیقاتی مواجه هستیم که گروهی از متغیرها در یک سمت و گروهی از متغیرها در سمت دیگر قرار دارند و ما قصد داریم همبستگی بین این دو مجموعه را به دست آوریم.

خوب مسلماً ضرایب همبستگی معمول و حتی تحلیل‌های علی مثل رگرسیون‌های چندگانه از انجام آن ناتوان هستند. در اینجاست که تحلیل همبستگی کانونی یا همان همبستگی بنیادی انجام این هدف را ممکن می‌سازد(گرین، 1978)

همبستگی کانونی یا همبستگی بنیادی برخلاف دیگر روش‌ها که تنها به بررسی هم‌تغییری دو متغیر می‌پردازد قادر است رابطه بین چند مجموعه از متغیرها را باهم بررسی نماید. علاوه بر این اگر بین مجموعه متغیرها دو یا سه رابطه وجود داشته باشد تکنیک همبستگی کانونی قادر به تشخیص و نشان دادن آن‌ها است(شری، 2005).

تحلیل همبستگی کانونی(همبستگی بنیادی) به‌عنوان درون داد اساسی خود با دو مجموعه متغیر که به هر یک از آن‌ها می‌توان یک معنای نظری داد سروکار دارد. استراتژی‌های اساسی آن عبارت است از استنتاج یک ترکیب خطی از مجموعه‌ای از متغیرها به‌گونه‌ای که همبستگی بین دو ترکیب خطی بیشینه شود(هومن، 1380).

 

مفاهیم اصلی تحلیل همبستگی کانونی(همبستگی بنیادی)

 

متغیرهای کانونی( Canonical variable)

درواقع شبیه به همان متغیرهای مکنون(پنهان) در مدل‌سازی معادلات ساختاری هستند و شامل نماینده جمع بهینه‌شده‌ی دو یا چند متغیر هست.

 

ضریب همبستگی کانونی( Canonical Correlation Coefficient)

ضریب همبستگی بین دو متغیر کانونی را ضریب همبستگی کانونی(همبستگی بنیادی) می‌گویند. همان‌طور که قبلاً گفته شد هر متغیر کانونی شامل ترکیب خطی یا نماینده جمع بهینه‌شده دو یا چند متغیر است(هایر و همکاران، 2006).

 

 تابع کانونی Canonical Function))

خوب تا اینجا آموختیم که هر متغیر کانونی شامل ترکیب خطی یا نماینده جمع بهینه‌شده دو یا چند متغیر است. حال همبستگی بین دو متغیر کانونی تشکیل تابعی به نام تابع کانونی می‌دهد(مرادی، 1395). مثلا متغیر کانونی مثل X از ترکیب خطی چند متغیر اصلی تشکیل می شود.

 

وزن‌های کانونی (Weight Canonical)

وزن کانونی درواقع سهم هر یک از متغیرهای اصلی در ضریب همبستگی کانونی یا بنیادی است. این وزن‌ها دقیقه مثل ضرایب رگرسیونی و ضرایب مسیر تفسیر می‌شوند.

 

بارهای کانونی (Canonical Loading)

همبستگی ساده خطی میان متغیرهای اصلی و متغیرهای کانونی متناظر آن‌ها است که همبستگی ساختاری نیز گفته می‌شود. درواقع می‌توان گفت متغیرهای کانونی شبیه همان متغیرهای مکنون و متغیرهای اصلی شبیه همان سؤالات و شاخص‌ها در تحلیل عاملی تأییدی است.

 

ریشه کانونی(Canonical roots)

این شاخص در حقیقت مجذور ضریب همبستگی کانونی(همبستگی بنیادی) هست. یعنی نشان می‌دهد که چقدر یک مجموعه از متغیرها می‌توانند رفتار مجموعه‌ای دیگر از متغیرها را پیش‌بینی و تبیین نمایند. این شاخص را مقدار ویژه نیز معرفی می‌کنند. اگر می‌خواهیم فهم دقیقی نسبت به آن داشته باشیم باید بدانیم که با ضریب تعیین در رگرسیون قابل‌مقایسه است.

در شکل زیر با تمامی مفاهیم گفته شده آشنا می شویم. در شکل زیر دو متغیر کانونی وجود دارند که خود از ترکیب خطی متغیر های متناظرشان تشکیل شده اند. همانطور که مشخص است متغیر کانونی محدودیت های سفر خود شامل مجموعه ای 4 تایی از متغیر های اصلی است و متغیر کانونی تصویر مقصد نیز خود شامل مجموعه ای 3 تایی از متغیر های اصلی است. وظیفه تکنیک همبستگی کانونی(همبستگی بنیادی) این است که رابطه ی این دو مجموعه را بدست آورد.

 

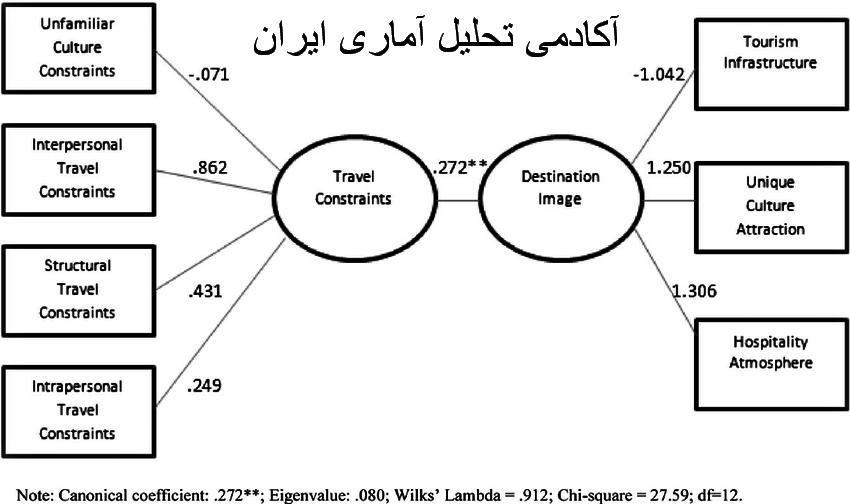
اگر به شکل دقت شود ضریب همبستگی کانونی 0.273 است و اگر آن را به توان 2 برسانیم در حقیقت ریشه کانونی را بدست آورده ایم. همچنین این مدل شامل 7 ضریب بار کانونی است که در حقیقت ضریب همبستگی هر متغیر اصلی را با متغیر کانونی متناظرش بدست می آورد.(مرادی، 1395).

این تحلیل از طریق نرم افزار های مختلفی قابل انجام است. در این مقاله به مسیر آن در نرم افزار spss اشاره می شود.

آدرس اجرای دستور در spss :

analyze……correlate……..canonical correlation                 

 

سپس در صفحه دیالوگ باز شونده در نرم افزار دو پنجره set1 و set2 را مشاهده می کنیم. متغیر های هر مجموعه را در پنجره خود وارد کرده و کلید ok را می زنیم. در نهایت نباید فراموش کرد که در مدل سازی معادلات ساختاری برای زمانی که تاثیر یک سازه مولفه دار را بر سازه ای مولفه دار دیگر می سنجیم در حقیقت با تکنیکی کامل تر همین کار را انجام می دهیم و ضریب مسیر بین دو سازه همان همبستگی کانونی بین دو سازه است. از دانشجویان آکادمی تحلیل آماری خواستارم کمی با دقت بیشتر به شیاهت ها و تفاوت های این دو تکنیک آماری توجه نمایند.

محسن مرادی

مطالب سایت و کانال بدون ذکر منبع سایت آکادمی در جای دیگر استفاده نشود.