تحلیل رگرسیون

تحلیل رگرسیون:

مفهوم رگرسیون برای اولین بار تسط فرانسیس  گالتون در سال 1877 مورد استفاده قرار گرفت. او در مطالعه خود نشان داد که قد کودکان متولد شده از والدین بلند قامت گرایش به برگشت به متوسط قد افراد جامعه دارد. او فرآیند پیش بینی یک متغییر از طریق یک متغییر دیگر را با مفهوم رگرسیون بیان کرد.

سپس رگرسیون چندگانه برای تخمین یا پیش بینی تغییرات یک متغییر به وسیله متغییرهای دیگر مورد استفاده قرار گرفت. از آن زمان به بعد تکنیک تحلیل رگرسیون برای تعیین رابطه آماری بین دو یا چند متغییر و پیش بینی  تغییرات یک متغییر از روی متغییر یا متغییرهای دیگر در سطح وسیع توسط محققان رشته های مختلف به کار گرفته شد.

همانطوری که قبلا نیز بیان گردید ضریب همبستگی که برای کشف وجود یا عدم وجود رابطه بین دویا چند متغییر به کار می رود از جمله روشهای تحلیلی است که علاوه بر تعیین شدت و ضعف رابطه بین دو متغییر، جهت را نیز نشان می دهد اما این روش قادر به بیان روابط علی بین متغییرها نبوده و نمی تواند کدامیک از متغییرها علت و کدامیک معلول دیگری است.

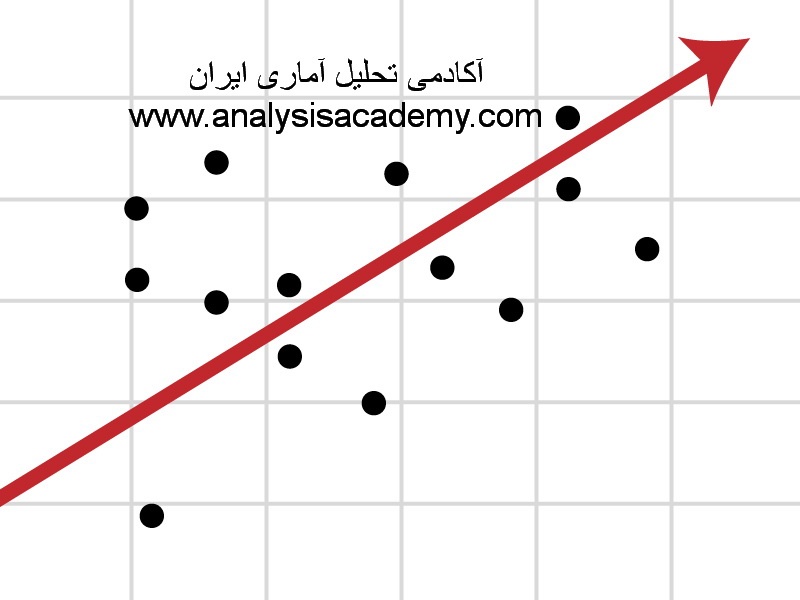
همچنین امکان پیش بینی یک متغییر از طریق متغییر یا متغییرهای دیگر وجود ندارد. به همین دلیل برای تحلیل های پیشرفته تر و پیش بینی تغییر در متغییر وابسته در صورت تغییر در متغییر یا متغییرهای مستقل باید از روش های دیگری نظیر تحلیل رگرسیون استفاده کرد. این روش ارتباط نزدیکی با ضریب همبستگی پیرسون و نمودار پراکنش داشته و خط رگرسیون در نمودار پراکنش مبنای تحلیل نقاط در این نمودار محسوب میشود و خط رگرسیون خطی است که مجموع مربعات انحراف نقاط روی نمودار با آن خط نسبت به هر خط دیگری حداقل مقدار را داشته و این خط مبنایی برای پیش بینی یک متغییر از طریق متغییر دیگر می باشد.

در تحلیل رگرسیون مقداری از واریانس متغییر Y را که بر مبنای متغییر X تبیین می گردد، مقدار واریانس تبیین شده می نامند که آن را R2 نمایش می دهند اگر مقدار R2 از 1 کم سود واریانس تبیین نشده به دست می آید.

معادله خط رگرسیون:

Y=a+bx

در این معادله:

Y=مقدار پیش بینی متغییر وابسته

a  = مقدار ثابت یا عرض از مبدا نقطه تقاطع خط رگرسیون با محور y

b = شیب خط یا ضریب رگرسیون

X=مقادیر متغییر مستقل