مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران
مدلهاي چند سطحي (multi level )در انواع علوم اجتماعي
تجزيه و تحليل چند سطحي جهت تحقيقاتي به كار مي روند كه در آن دو يا سه سطح مختلف در ايجاد يك مشكل و يا يك پديده مطلوب دخالت دارند. نحوه دخالت نيز به گونه اي است كه يك عامل يا علت از سطح بالاتر به عنوان متغير تعديل كننده در رابطه اثر گذاري دو متغير مستقل و وابسته در سطح پايين تر اثر گذاشته و موجب تشديد و يا تضعيف اين رابطه مي شود.
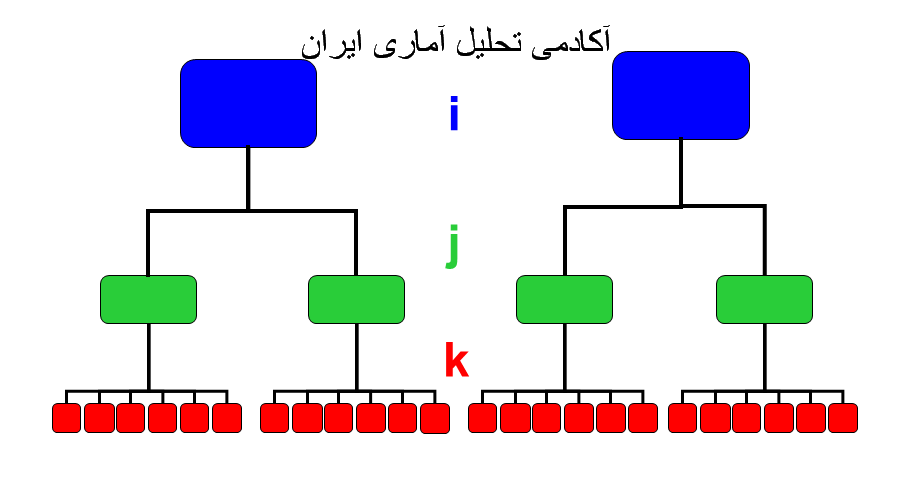
به عنوان مثال مي توان در يك سازمان چنين فرض كرد كه ميزان دستمزد بر روي انگيزش كاركنان اثر مثبت مي گذارد يعني با افزايش دستمزد مي توان انتظار داشت كه انگيزه كاركنان افزايش مي يابد. حال ممكن است متغير ديگري به عنوان شهرت سازمان به عنوان متغيري كه در سطح بالاتر يعني در سطح سازمان قرار دارد بر روي اين رابطه اثر بگذارد يعني شهرت بالاتر سازمان موجب شود كه رابطه مثبت بين ميزان دستمزد و انگيزه كاهش پيدا كند. براي اينكه بتوانيم مقدار و شدت اين اثر گذاري متغير سطح بالاتر را بر روي رابطه دو متغير سطح پايين تر اندازه گيري كنيم مي بايست از تجزيه و تحليل و مدلسازي چند سطحي استفاده كنيم.لازم به ذكر است كه در اين تحليل ها منظور از سطح بالاتر نمونه هايي است كه از مجموع چندين نمونه سطح پايين تشكيل شده است. به عنوان نمونه مي توانيم صنعت ، شركت و كارمندان را به ترتيب سطح 3 و 2 و 1 تعريف كنيم چرا كه مجموع چند كارمند ( سطح 1 ) باشند در يك نمونه سطح 2 ( شركت ) قرار داشته و مجموع چند نمونه سطح 2 ( شركتها) تشكيل يك صنعت را (كه سطح بالاتر يعني سطح 3 ) باشند را مي دهند.
بنابراین مدلهاي چند سطحي هنگامی تشکیل می‌شوند که بتوان داده‌ها را در دسته‌های مختلف جای داد. به عنوان مثالی دیگر دانش آموزان را می‌توان در کلاس‌ها، بیماران را در بیمارستان و استادان را در دانشکده‌ها طبقه‌بندی نمود. در این نوع مدلسازی به دانش آموز، بیمار و استاد سطح 1 و به کلاس، بیمارستان و دانشکده سطح 2 گفته می‌شود. در صورتی که بتوان عناصر سطح 2 را دوباره در یک مجموعه دیگر طبقه‌بندی نمود آنگاه سطح 3 نیز وجود خواهد داشت. در مثال‌های ما سطح 3 می‌تواند مدرسه، دانشگاه علوم پزشکی و دانشگاه باشد.
داده‌های سطح 1 در هر طبقه‌ای که قرار می‌گیرند دارای ویژگی‌های مشابهی هستند. به عنوان مثال دانش آموزانی که در یک کلاس هستند همگی دارای یک معلم مشترک هستند.
در مدل‌های چند سطحی همواره یک متغیر از سطح بالاتر به عنوان یک متغیر مداخله‌گر بر رابطه رگرسیونی بین دو متغیر در سطح پایین‌تر اثر می‌گذارد.
از آنجا که قرار است در مدل چند سطحی اثر یک یا چند متغیر سطح بالاتر(تعداد ساعات آموزش کلاس و تعداد دانش‌آموزان کلاس) در رابطه رگرسیونی فوق مورد بررسی و آزمون قرار گیرد بنابراین به سه شرط نیاز داریم:
الف) دارای چندین گروه از سطح بالاتر(چندین کلاس) باشیم که در هر گروه چندین نمونه داده از سطح پایین تر (دانش آموز) موجود باشد که هر نمونه دارای اطلاعات در مورد متغیرهای وابسته (نمره‌ای که این دانش‌آموز گرفته) و مستقل (میزان زمانی که این دانش آموز درس خوانده است) باشد.
ب) رابطه رگرسیونی مذکور را برای هر گروه (در اینجا کلاس) به صورت جداگانه حساب کنیم و بنابراین به تعداد متغیر سطح بالاتر دارای فرمول رگرسیونی خواهیم بود که طبیعتا به همان تعداد عدد ثابت و ضریب رگرسیونی خواهیم داشت.
ج) از آنجا که در یک مدل چند سطحی در پی محاسبه و آزمون اثر متغیر سطح بالاتر (تعداد ساعات آموزش کلاس و تعداد دانش آموزان کلاس) بر رابطه رگرسیونی سطح پایین‌تر هستیم و از آنجا که چگونگی رابطه رگرسیونی سطح 1 به دو عامل عدد ثابت و ضریب رگرسیونی آن بستگی دارد پس در واقع در روابط جدید که ایجاد می‌شود متغیر سطح بالاتر به عنوان متغیر مستقل قرار گرفته و یکبار عدد ثابت و بار دیگر ضریب رگرسیونی سطح 1 به عنوان متغیر وابسته خواهد بود.
