سطوح اندازه گیری

سطوح اندازه گیری:

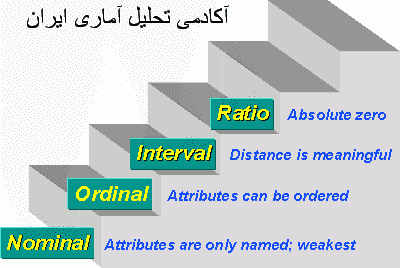
برخلاف علوم طبیعی فرآیند اندازه گیری در علوم اجتماعی و انسانی کار بسیار پیچیده ای بوده و علیرغم پیشرفتهای عمده ای که در این حوزه انجام گرفته است هنوز سنجش و اندازه گیری در این بخش از دقت لازم برخوردار نمی باشد.از آنجا که کاربرد روشهای آماری مختلف در تحقیقات اجتماعی-اقتصادی تحت تاثیر نوع و طبیعت داده های موجود می باشد، بنابراین آشنایی با سطوح اندازه گیری،محقق را در انتخاب روشهای آماری مناسب برای توصیف و تحلیل داد ها کمک خواهد کرد. مفاهیم و متغییرهای مورداستفاده در علوم اجتماعی و انسانی با چهار مقیاس سنجیده می شوند. که از نظر میزان دقت به سطوح اسمی، ترتیبی، فاصله ای، نسبی تقسیم می گردند.

1-سطح اسمی

این سطح ابتدایی ترین سطح اندازه گیری است که در آن مقولات یک متغییر به صورت قراردادی در کنار یکدیگر قرار می گیرند تا چگونگی همسانی یا ناهمسانی آنها مشخص شود مانند جنسیت: 1)زن،2)مرد یا محل تولد:1)تهران،2)تبریز،3)شیراز،4)اصفهان

در این سطح از اندازه گیری فقط هر مقوله از مقوله دیگر متمایز می شود و هر فرد مورد بررسی فقط در یکی از این مقولات قرار می گیرد و اعدادی که به مقولات یک متغییر اختصاص داده می شود ارزش حقیقی عدد را ندارد.به عنوان مثال نمی توان گفت که مرد دو برابر زن است و یا شیراز سه برابر تهران است. زیرا ترتیب قرار گرفتن مقولات امری قراردادی است در این سطح از اندازه گیری تنها می توان به محاسبه فراوانی، درصد و نما یا مد اکتفا کرد.

سطح ترتیبی:

در سطح ترتیبی اندازه گیری یک پله بالاتر می رود یعنی علاوه بر همسانی و ناهمسانی مقولات، ترتیب آنها هم مشخص می شود و این ترتیب  هم واقعی و هم منطقی است. مثال میزان علاقه به تحصیل:1)کم،2)متوسط،3)زیاد یا طبقه اجتماعی:1)پایین،2)متوسط،3)بالا

در این سطح از اندازه گیری جهت تغییر از کم به زیاد ی از ضعیف به شدید است. بنابراین در این سطح علاوه بر همسانی یا ناهمسانی مقولات شدت و ضعف و ترتیب آنها نیز مشخص می شود. ولی چون فواصل بین مقولات مشخص نیست، اعداد اختصاص یافته به مقولات باز هم فاقد ارزش عددی است. یعنی نمی توانیم بگوییمکه فلانی سه برابر دیگری به تحصیل علاقه دارد بلکه تنها می توانیم او را از افراد کم علاقه متمایز کنیم و شدت علاقه او را مشخص کنیم.

برای داده هایی کهدر سطح ترتیبی جمع آوری شده اند تنها می توان به تعیین توزیع فراوانی، درصد، مد یا نما و ضریب همبستگی کندال اکتفا کرد و چنانچه داده ها به صورت رتبه ای باشد یعنی از سلسله اعداد طبیعی 1،2،3 و … تبعیت کنند در اینصورت می توان از آماره هایی نظیر میانه وضریب همبستگی رتبه ای اسپیرمن نیز استفاده کرد.

سطح فاصله ای:

در این سطح علاوه بر تعیین سطوح مختلف و ترتیب منطقی و واقعی بین مقادیر متغییر فاصله بین مقادیر فوق نیز مشخص است مانند هزینه خانوار یا نمره دانشجو. در این سطح می توانیم نمره یک دانشجو را از دانشجوی دیگر متمایز کنیم . کمی یا زیادی آن را مشخص کنیم و فاصله آن را نیز از دیگر مقادیر متغییر تعیین کنیم. به عنوان مثال می توان گفت که دانشجویی که نمره 20 دریافت کرده است با دانشجویی که نمره 10 گرفته است به اندازه 10 نمره فاصله یا اختلاف دارد.

اما در این مقیاس صفر مطلق وجود ندارد. به عنوان مثال اگر دانشجویی در درس آمار صفر گرفته باشد نباید فرض کرد که اصولا فاقد دانش آمار است. برای داده هایی با مقیاس فاصله ای شاخص هایی از قبیل میانگین، انحراف معیار،واریانس و ضریب همبستگی پیرسون قابل محاسبه هستند و انجام آزمونهای Tو F و غیره نیز امکانپذیر است.

سطح نسبی:

بالاترین و دقیق ترین سطح اندازه گیری است که علاوه بر تعیین سطوح  و مقادیر یک متغییر و تعیین فاصله بین مقادیر یک متغییر نسبتها نیز قابل محاسبه و بیان هستند و مبنای اندازه گیری نیز صفر مطلق است مانند مقدار پول در حساب دانشجو، یا میزان درآمد . در این متغییر اگر حساب دانشجو صفر باشد، واقعا هیچ پولی در حساب او نیست زیرا این متغییر دارای صفر مطلق است و وجود صفر حقیقی به عنوان مبدا اندازه گیری محقق را قادر می سازد تا از روشهای مختلف استفاده کند. برای داده های این مقیاس علاوه بر اینکه کلیه شاخص های ذکر شده در سطح فاصله ای قابل محاسبه می باشند بلکه شاخص هایی نظیر میانگین هندسی و ضریب پراکنش که به صفر حقیقی نیاز دارند نیز قابل محاسبه است.