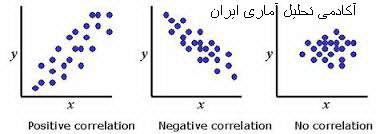
یادگیری ضریب همبستگی[1]، کارکرد و انواع آن از اولین ملزومات به کارگیری روشهای محاسباتی در تحقیقات علی – معلولی می باشد . ضریب همبستگی مبنای محاسبات مربوط به تحلیل مسیر[2] و در نتیجه معادلات ساختاری[3] می باشد. ضريب همبستگي ارتباط بین دو متغیر را نشان می دهد.این ضریب ابزاری است آماری که به وسیله آن می توان درجه ای را که یک متغیر به متغیر مرتبط است را اندازه گیری کرد.
توضیحات بیشتر »اصول اوليه تحليل مسير در آمار و روش تحقيق
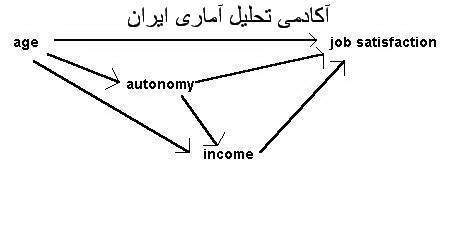
تحليل مسير يا path analysis روش آماري كاربرد ضرايب بتاي استاندارد رگرسيون چند متغيرى در مدل هاى ساختاري است هدف تحليل مسير به دست آوردن برآوردهاى كمى روابط علّى ( همکنشي يکجانبه يا کواريته) بين مجموعه اى از متغيرهاست.ساختن يک مدل علّي لزوماً به معناي وجود روابط علّي در بين متغيرهاي مدل نيست بلکه اين عليت بر اساس مفروضات همبستگي و نظر و پيشينه تحقيق استوار است.
توضیحات بیشتر »ماتریس ارزیابی و نقشه ادراکی
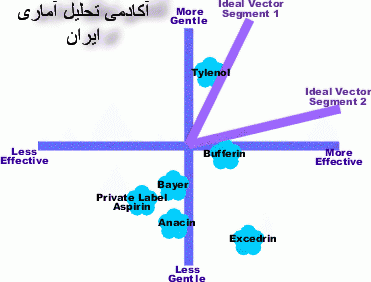
نقشه های ادراکی (Perceptual Map) یکی از ابزارهای مدیریت استراتژیک هستند که عمری حدود 30 سال دارند. نقشه های ادراکی به مدیران کمک می کنند تا بتوانند ارتباط پیچیده ی بین رقبای بازار و معیارهای مصرف کنندگان در تصمیم گیری برای خرید را درک کنند. این ابزار قدرتمند می تواند یک پشتیبان قوی برای تصمیمات استراتژیک پیرامون محصول و بازاریابی باشد.
توضیحات بیشتر »FIMIX در حداقل مربعات جزئی
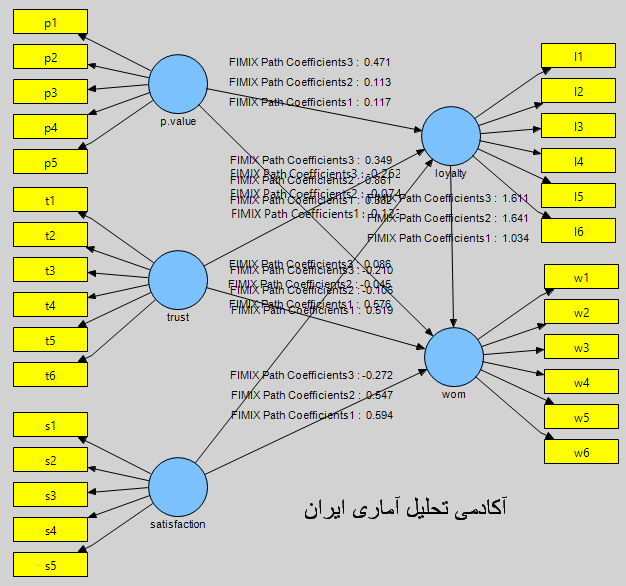
این ناهمگنی در جامعه مورد مطالعه اغلب به خاطر وجود ادراکات و برداشت های متفاوت افراد مختلف از از موضوعات متفاوت است و اغلب در تحقیقات نگرش سنجی در مدیریت، بازاریابی و علوم اجتماعی و روانشناسی و غیره کاملا ملموس است. رویکرد FIMIX جامع ترین و رایج ترین رویکرد برای برخورد با ناهمگنی در مدل سازی مسیری PLS است.
توضیحات بیشتر »تفاوت روشهای کمی تصمیم گیری TOPSIS و AHP
در علم تصميمگيري كه در آن انتخاب يك راهكار از بين راهكارهاي موجود و يا اولويتبندي راهكارها مطرح است، چند سالي است كه روشهاي تصميم گيري با شاخصهاي چند گانه «MADM» جاي خود را باز كردهاند. از اين ميان روش تحليل سلسله مراتبي (AHP) بيش از ساير روشها در علم مديريت مورد استفاده قرار گرفته است. فرايند تحليل سلسله مراتبي يكي از معروفترين فنون تصميم گيري چند معیاره است كه اولين بار توسط توماس ال. ساعتي عراقي الاصل در دهه 1970 ابداع گرديد. فرايند تحليل سلسله مراتبي منعكس كننده رفتار طبيعي و تفكر انساني است. اين تكنيك، مسائل پيچيده را بر اساس آثار متقابل آنها مورد بررسي قرار ميدهد و آنها را به شكلي ساده تبديل كرده و به حل آن ميپردازد.
توضیحات بیشتر »آمار توصیفی یا ارائه داده ها
کلمه آمار ابتدا به معنی مجموعه اطلاعاتی از جمعیت واقتصاد بود، اینک، آمار از آن شروع ابتدایی ، به یک روش علمی تجزیه و تحلیل که در تمام رشته های علوم اجتماعی ومهندسی و... به کار برده میشود،ترقی کرده است. آمار شاخه ای از علوم است که به نقش: 1-سازماندهی وخلاصه کردن 2-استنباط ونتیجه گیری در باره مجموعه ای از داده هاست ،وقتی که تنها بخشی از آن ها مشاهده شده اند. درحقیقت آمار یک روش است که هدفش توصیف کردن است وعلاوه بر این ، یک روش کمی است که از عدد به عنوان وسیله ای برای بیان و توصیف استفاده میشود. با نگرش به این توصیف ، از نقطه نظر آموزشی ، سه مرحله زیر را میتوان در آمار در نظر گرفت: 1-آمار توصیفی 2-احتمالات 3-آمار ریاضی
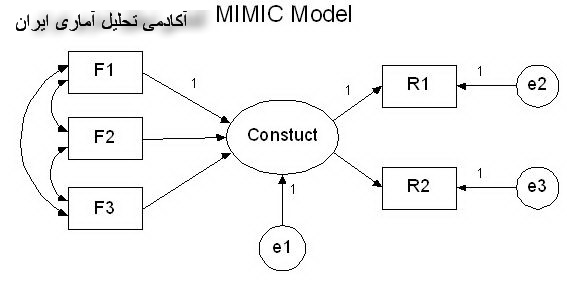
توضیحات بیشتر »مدل MIMIC
مدل MIMIC در مدل سازی معادلات ساختاری ترکیبی از مدل های انعکاسی و ترکیبی است که به مدل های ساختاری با معرف های چندگانه و علل چند گانه شهرت دارد.
توضیحات بیشتر » مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران
مدرسه بین المللی پژوهش کمی و کیفی اولین و بزرگترین مرکز بین المللی برگزارکننده دوره های روش پژوهش و نرم افزارهای پژوهش کمی، کیفی، آمیخته و مروری در ایران